Partimos del número, phi Φ, un número irracional que fue dado a conocer por Euclides, quien escribió sistemáticamente sobre él a principios del siglo IV aC. Y aunque pudiera parecer que la magia evocada por el pentáculo y el pensamiento matemático del número áurico no tuvieran nada que ver, no es así y el mejor ejemplo lo encontramos en el propio John Dee, quien tradujo el libro de Euclides al inglés y lo enriqueció con sus comentarios [1]. Un poco antes, en 1546, Dee escribió la Monas Hieroglyphica, su obra más importante, redactada según el sistema matemático de postulados continuos, en ella, Dee buscaba resumir en una figura todo el pensamiento mágico que para él no era distinto del matemático.
John Dee tradujo el libro de Euclides y lo enriqueció con sus comentarios, antes, había escrito la Monas Hieroglyphica redactada según el sistema matemático de postulados continuos y en la que buscaba resumir en una figura todo el pensamiento mágico que para él no era distinto del matemático.
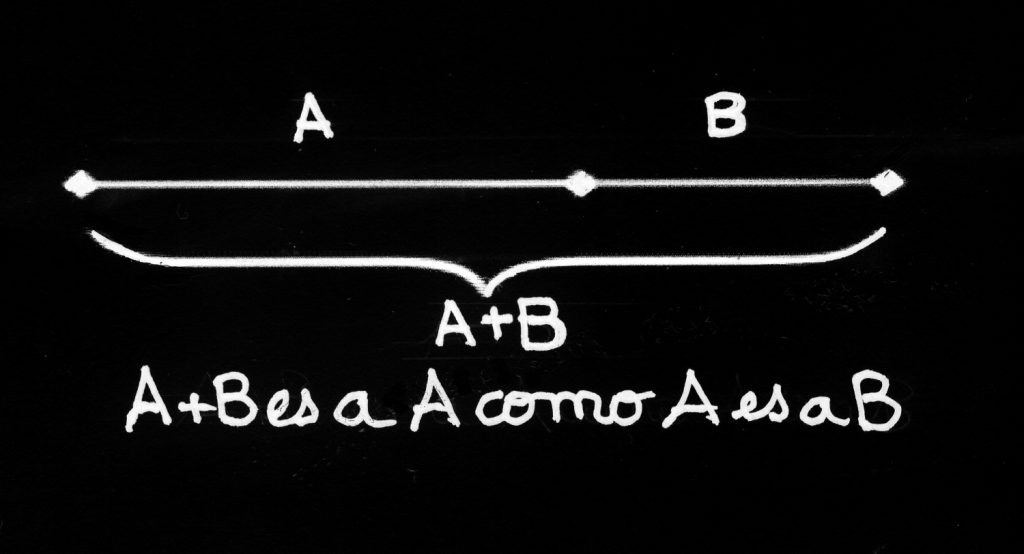
Para los seguidores de Euclides, y también para los renacentistas, conocer el número irracional phi significaba poseer la llave del orden perfecto, penetrar en la armonía de las formas creadas por la naturaleza y, en consecuencia, crear según el patrón de la sabiduría natural, que se obtiene a partir de las matemáticas, y que conduce a la belleza en la naturaleza y el arte. Un sistema en el que, además, la Unidad se pueda dividir de tal modo que no pierda su esencia de unidad. Si se divide una recta, o un rectángulo, por la mitad, simétricamente, como se hizo, por ejemplo, en el arte medieval, es un modo simple de lograrlo, pero hay otra manera, y es la que Euclides expresó por medio del número phi, y que definió del modo siguiente: “Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor” [2].
Si la relación entre la parte menor y la mayor de una unidad es la misma que entre la parte mayor y la unidad primera, la creación, que es la multiplicación de la Unidad, deja de ser un caos en el que cada parte es y actúa arbitrariamente sin coordinarse con las otras, para convertirse en orden. Según la propuesta euclidiana, al mantenerse la proporcionalidad de las partes se demuestra que en la creación y en la multiplicidad también puede existir el orden.
Si la relación entre la parte menor y la mayor de una unidad es la misma que entre la parte mayor y la unidad primera, la creación, que es la multiplicación de la Unidad, deja de ser un caos en el que cada parte es y actúa arbitrariamente sin coordinarse con las otras, para convertirse en orden.
No es de extrañar que se viera la actuación de lo divino en el número phi, de tal modo que, las matemáticas, como base de todas las ciencias, se consideraron sagradas puesto que permitían comprender y desarrollar sus operaciones.
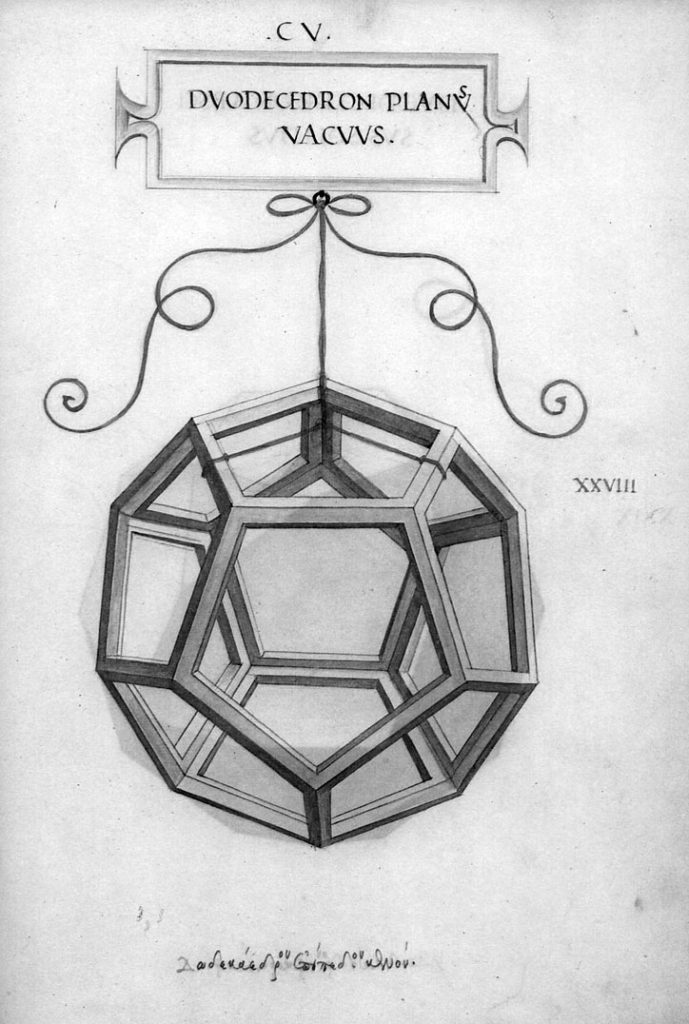
Durante el Renacimiento italiano del siglo XV y de la mano de Luca Pacioli, quien escribió La divina proporción, la búsqueda de los sistemas armónicos antiguos fue un verdadero camino donde se encontraron el arte y la ciencia, o, también, la música y la matemática –como sucedía antiguamente en las escuelas pitagóricas. Leonardo da Vinci, que coincidió con Pacioli en la corte milanesa, ilustró la parte del libro donde se explica la manera de construir los sólidos platónicos.
El motivo por el que Pacioli llamó divina proporción a la aritmética y a la geometría que se genera a partir del número phi, lo explica al principio de su obra y aunque lo hace desde una óptica cristiana –Pacioli era fraile franciscano–, muestra el sentimiento general de los humanistas; así, según Pacioli: “El título conveniente a nuestro tratado ha de ser el de Divina Proporción, y ello por numerosas correspondencias de semejanza que encuentro en nuestra proposición, de la que tratamos en este nuestro utilísimo discurso, que corresponden a Dios mismo” [3] y continúa: “Para nuestro propósito será suficiente considerar cuatro de ellas, entre otras. La primera es que la proporción es una sola y no más, y no es posible asignarle otras especies ni diferencias. Y dicha unidad es el supremo epíteto de Dios mismo, según todas las escuelas teológicas y también filosóficas” [4]. Después establece una relación entre las tres segmentos que participan en la divina proporción con la Santísima Trinidad y lo explica del modo siguiente: “así como in divinis hay una misma sustancia entre tres personas –Padre, Hijo y Espíritu Santo– de igual modo una misma proposición se encontrará siempre en tres términos, y nunca en más o menos, como se dirá” [5].
El motivo por el que Pacioli llamó divina proporción a la aritmética y a la geometría que se genera a partir del número phi, lo explica al principio de su obra y aunque lo hace desde una óptica cristiana, muestra el sentimiento general de los humanistas renacentistas.
Otra razón que hace que la proporción euclidiana sea divina es porque es un misterio, pues del mismo modo que: “Dios no se puede propiamente definir ni puede darse a entender a nosotros mediante palabras, nuestra proporción no puede nunca determinarse con números inteligibles ni expresarse mediante cantidad racional alguna, sino que siempre es oculta y secreta y es llamada irracional por los matemáticos” [6]. La cuarta propiedad es la que considera que: “en toda cantidad continua y discreta, grande o pequeña es la misma y siempre invariable, y de ninguna manera puede cambiar ni de otro modo puede aprehenderla el intelecto”. Finalmente, la proporción es divina pues es la quintaesencia del cielo y de la tierra [7].
La quintaesencia y los cuatro elementos han sido representados geométricamente con los llamados cuerpos regulares o cuerpos platónicos. En un curioso libro de perspectiva realizado por Wentzel Jamnitzer y titulado Perspectiva Corporum Regularium [8] , el autor hace un ejercicio de virtuosismo al mostrar las distintas posibilidades de representación de los cuerpos, a los que además relaciona con las cinco vocales y los cinco elementos. El primer cuerpo corresponde al tetraedro, a la vocal A y al elemento fuego. Al octaedro le corresponde la letra E y el elemento aire. El exaedro se relaciona con la vocal I y el elemento tierra. El icosaedro con la vocal O y el elemento agua. Finalmente, el dodecaedro corresponde a la última vocal, la U, y representa el cielo, como una quintaesencia, pues esta figura está relacionada con el número cinco. Tiempo después, el grabador Albert Flocon se quedó fascinado con este libro y expresó su admiración con las siguientes palabras: “La belleza severa de las láminas es tal, su materialidad metálica tan palpable, que realmente Jamnitzer tenía derecho a decir, cándidamente maravillado, ‘que parecía imposible que cada uno de esos objetos pudiera ser obra de la mano del hombre’” [9].
La belleza sería la práctica sensible de una teoría razonante, de manera que el uso de la divina proporción consigue explicar aquello que es bello, argumentándolo matemáticamente. La belleza no es la consecuencia, dirían los renacentistas, de una sensibilidad especial ni de ningún azar, sino que aparece en el mundo gracias a la identidad del hombre con el Creador. Identidad que pasa, obviamente, porque el hombre utilice la misma regla que el Creador: la divina proporción.
La belleza no es la consecuencia, dirían los renacentistas, de una sensibilidad especial ni de ningún azar, sino que aparece en el mundo gracias a la identidad del hombre con el Creador. Identidad que pasa, obviamente, porque el hombre utilice la misma regla que el Creador: la divina proporción.
Esta teoría se inscribe en el sueño del Renacimiento por encontrar el símbolo universal, aunque no alcanza a explicar todos los sistemas de armonía y creación. Muchos grandes pintores de la época no utilizaron esta proporción en sus obras, mientras otros artistas que sí la utilizaron, solo alcanzaron obras mediocres. Pero el espíritu renacentista se asentaba en la idea de que todo el arte de la Antigüedad estaba basado en la regla dorada y, por eso, ésta debía ser el referente obligado. Tal idea perduró durante el mundo moderno, con más o menos fuerza según iban cambiando los estilos de cada época, hasta que, a finales del siglo XIX y comienzos del XX, reapareció con nuevo vigor, sobre todo con el libro de Adolf Zeising, titulado Aesthetische forschungen y publicado en 1855, en el que se recuperaron las enseñanzas renacentistas.
Sin embargo, en los círculos masónicos se mantuvo el estudio de la divina proporción de manera continuada desde la época de John Dee. Sus logias se reconocían continuadoras de las escuelas secretas de Pitágoras, y así lo explica el belga Jean Mallinger en su estudio sobre la tradición pitagórica, donde relata con todo detalle la leyenda de la ininterrumpida continuidad de la transmisión secreta del misterio de los números dentro de las logias [10]. Estos grupos, como es lógico, estuvieron muy interesados por la armonía que se desprendía de la arquitectura clásica, especialmente de los templos griegos, pues los veían como ejemplos de la divina proporción y como modelos para sus templos masónicos.
Las logias masónicas se reconocían continuadoras de las escuelas secretas de Pitágoras, y así lo explica Jean Mallinger en su estudio sobre la tradición pitagórica, donde relata la leyenda de la ininterrumpida continuidad de la transmisión secreta del misterio de los números dentro de la masonería
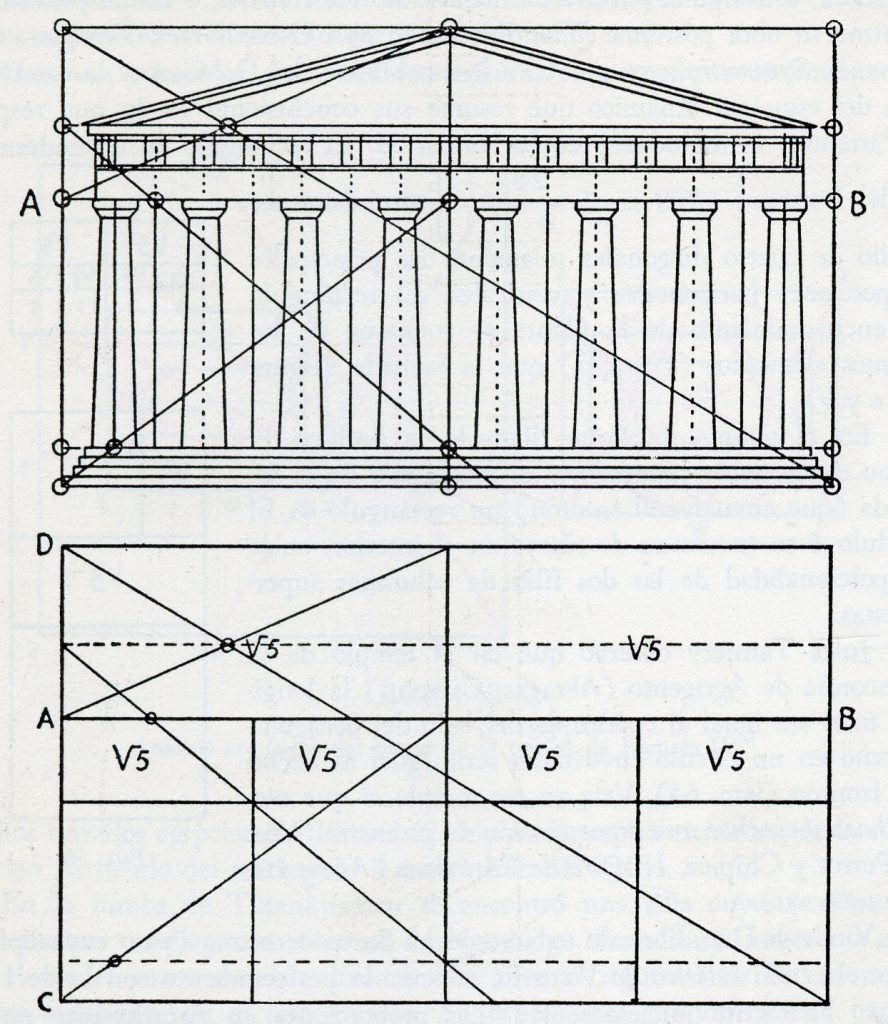
Por su significado dentro de la historia del arte, el Partenón ha sido el edificio que más se ha analizado, sobre todo, a partir de los estudios que en los años veinte del siglo pasado realizó el artista americano Jay Hambidge y que se publicaron póstumamente, en 1926, bajo el título The Elements of Dynamic Symmetry. Otros autores, como Matila C. Ghyka, los recuperaron y ampliaron con auténtica pasión; es fundamental en este sentido su Estética de las proporciones en la naturaleza y el arte, pues es el inicio de una larga bibliografía sobre el número phi, en él, Ghyka cita a Hambidge, pero se lamenta de no haber podido consultar su obra y tener que explicar el esquema dinámico del Partenón gracias a la amabilidad del Dr. Caskey [11]. El caso es que ambos autores muestran el conjunto de fuerzas dinámicas y armónicas del edificio “más bello” que ha creado el hombre.
Un poco antes de la aparición del libro de Adolf Zeising, concretamente en 1851, Johann Georg Heck publicó The Complete Encyclopedia of Illustration, una vasta obra universal en la que la pasión por el mundo clásico surge de la mezcla inevitable entre el romanticismo y el clasicismo de aquellos años. El grabado que ilustra la ciudad de Atenas es magnífico; realista a su modo, pues exalta lo que le gustaba al autor: el Partenón, pero esta visión también desvela el sentido simbólico de la Acrópolis.
Acrópolis significa “ciudad elevada” y era la morada de Palas Atenea, Heck la representa sobre un monte más alto de lo que debería ser en realidad, pero que permite entender su función como residencia de los dioses, de modo que toda la gran arquitectura, escultura y pintura que conformaba el conjunto de la Acrópolis tenía como finalidad realzar el lugar apartado del mundo profano, representado por la montaña, desde donde la hija de Zeus ordenaba asuntos de su ciudad. De esta arquitectura destaca, obviamente, el Partenón donde se encontraba la famosa estatua de Fidias.
Toda la gran arquitectura, escultura y pintura que conformaba el conjunto de la Acrópolis tenía como finalidad realzar el lugar elevado apartado del mundo profano, representado por la montaña, desde donde la hija de Zeus ordenaba asuntos de su ciudad.
El Partenón, como los demás templos griegos, también buscaba reproducir la imagen de la elevación de la tierra pura, por eso, el conjunto visto desde el exterior consta de dos partes: las columnas y los frontones donde se desarrollan las escenas mitológicas. En el frontón situado al este se representa el nacimiento de Palas Atenea y en el del oeste, su disputa con Poseidón. El triángulo de los frontones sobre la base cuadrangular de las columnas simbolizaría su sublimación, y se le atribuye el mismo sentido que el de la cumbre de la montaña.
Para comprender el simbolismo que subyace en el Partenón quizá sea útil un acercamiento al lenguaje de la Masonería. Los tres grados básicos de su proceso son: aprendiz, compañero y maestro. A cada grado le corresponde un tipo de piedra –en el sentido de un objeto arquitectónico–; el aprendiz está relacionado con la piedra bruta, es decir, la materia sin pulir ni trabajar, cosa que él mismo deberá hacer hasta alcanzar la piedra cúbica, una piedra tallada y preparada para servir en la construcción del templo; esta segunda piedra corresponde al grado de compañero. Finalmente, el grado de maestro se asocia a la piedra cúbica en punta, es decir, el cubo perfecto sobre el que se levanta una pirámide, imagen del cuaternario sublimado. Este proceso permite penetrar en el sentido simbólico de los frontones de los templos griegos y también en el las montañas donde se levantan, todos ellos son imágenes de la materia sublimada.
Para comprender el simbolismo del Partenón quizá sea útil un acercamiento al lenguaje de la Masonería. Los tres grados básicos de su proceso son: aprendiz, compañero y maestro. A cada grado le corresponde un tipo de piedra, la piedra bruta, la cúbica y la pirámide, el cubo sublimado.
La idea de Hambidge era la de aplicar la particular manera de formar rectángulos áuricos a los trazados del Partenón. Los rectángulos áuricos son dinámicos por varias razones, pero, sobre todo, porque se pueden subdividir infinitamente manteniendo siempre la unidad y creando un desarrollo que se ha comparado con la sucesión de Fibonacci. Lo importante de la sucesión ideada por Leonardo de Pisa, conocido como Fibonacci, es que todas las formas creadas por la naturaleza y el hombre siguen la misma pauta. Incluso, o, sobre todo, el cuerpo del hombre. El caparazón de un fósil de caracol es un icono de una belleza que, por azar o necesidad, ha surgido de la evolución; como es lógico, responde a la sucesión de Fibonacci y también a la proporción del número phi. Una fotografía de Manel Armengol de una serie llamada Piedras del cielo, muestra su belleza y misterio.
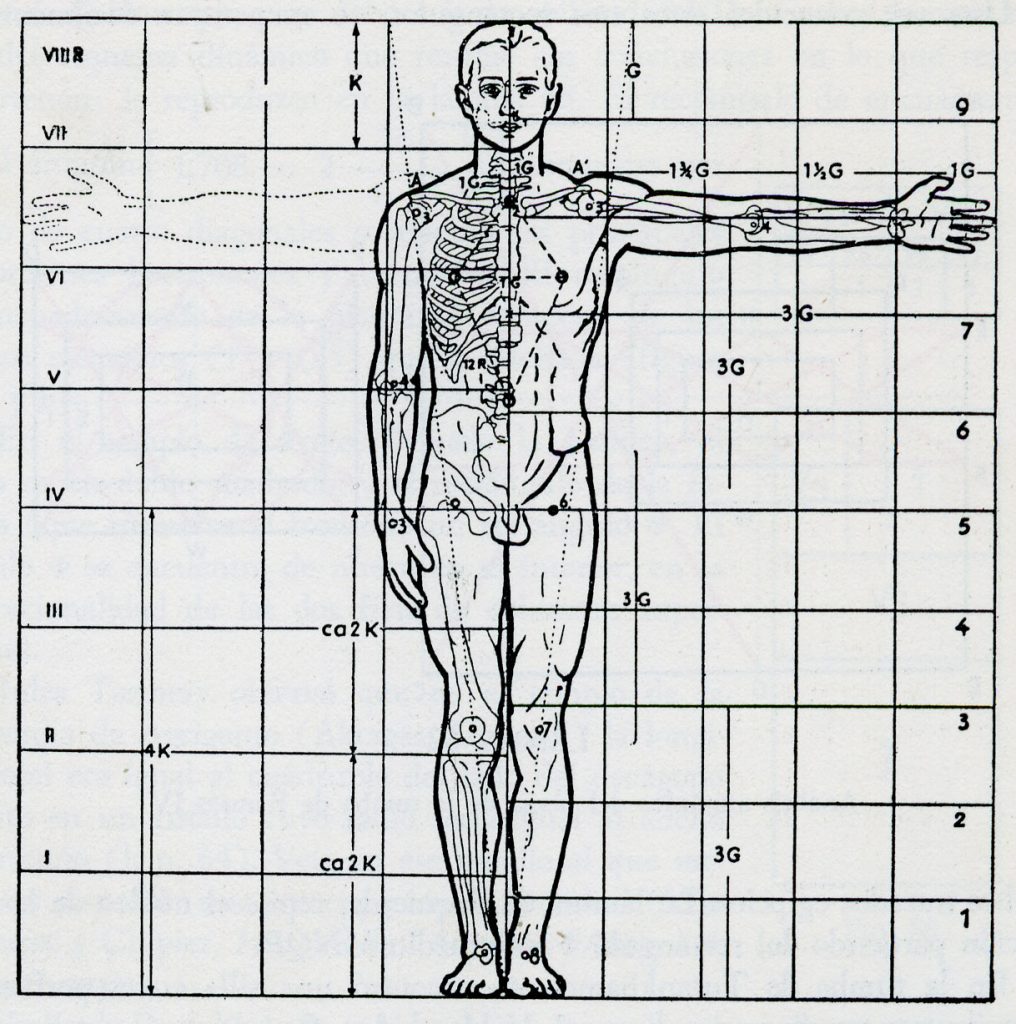
A las propuestas matemáticas que fundamentan el pensamiento simbólico contemporáneo, se debe añadir la estela abierta por el psicólogo alemán Gustav Theodor Fechner quien, en 1860, publicó Elemente der Psychophysik y estableció una disciplina, la psicofísica, que relaciona las escalas físicas de los estímulos con la escala de las sensaciones que recibe el sujeto. Uno de los experimentos más conocidos era el de presentar a un público muy variado distintos rectángulos y comprobar cuál era el que mayoritariamente era considerado el más bello. El construido a partir de la divina proporción fue el escogido, con lo que se demostraba el origen matemático de la belleza. Estos experimentos son la consecuencia lógica de la necesidad de aunar la creación y el Creador por medio de un canon que explique el orden sagrado. Y este canon debe manifestarse también en el microcosmos, es decir, en el cuerpo humano, hecho a imagen y semejanza de Dios. Así la psicofísica de Fechner es una continuación natural de la búsqueda de los cánones de la belleza.
Uno de los experimentos más conocidos es el de presentar a un público muy variado distintos rectángulos y comprobar cuál era el que mayoritariamente era considerado el más bello. El construido a partir de la divina proporción fue el escogido, con lo que se demostraba el origen matemático de la belleza.
Este empeño encontró en los artistas y pensadores del Renacimiento su culminación, pues según la filosofía neoplatónica de Pacioli o Durero, la belleza o la armonía de un cuerpo o de un rostro, debía seguir el dictado de los cánones derivados de la divina proporción. Sin embargo, lo comprobamos cotidianamente, la belleza persiste al margen de todo ello, se trata de un misterio insondable. El libro de Durero, titulado Cuatro libros sobre las proporciones humanas, y publicado póstumamente en1528, va mucho más allá de un tratado de geometría, pues recoge los dibujos y estudios del artista alemán durante sus veinte años de investigación sobre el símbolo del hombre- Es una obviedad, a menudo marginada, que Durero quería trasladar al cristianismo, y en especial a la imagen de Jesucristo, los presupuestos de la belleza clásica, pues no comprendía por qué, en el mundo clásico, podía representarse un ídolo como Apolo con tanta belleza y, en cambio, la icona del Dios auténtico fuera de factura muy inferior.
Siglos más tarde, William Blake se refirió a la representación de Dios como un hombre, es decir, la concepción antropomórfica de Dios, lo divino humano en palabras del poeta y pintor visionario, que añade: “Dios aparece y Dios es Luz / para esas pobres Almas que moran en la Noche, / pero se despliega una Forma Humana / para aquellos que moran en los Reinos del día” [12].
LIBRO
NOTAS
- [1] Dee, John. The Mathematicall Praeface to the Elements of Geometrie of Euclid of Megara (1570).
- [2] Elementos. Libros V-IX, Gredos, Madrid 2012; p. 203.
- [3] La divina proporción, Akal, Madrid 1991; p. 41.
- [4] Ibídem.
- [5] Ibídem.
- [6] Ibídem.
- [7] Ibídem.
- [8] Perspectiva Corporum Regularium, Siruela, Madrid 1993.
- [9] Ibídem; p. 21.
- [10] Pythagore et les Mystères, Planquart, Lille 1974; pp. 13-35.
- [11] Estética de las Proporciones en la Naturaleza y en las artes, Poseidón, Barcelona 1979; pp. 201-2.
- [12] Citado por Kathleen Raine en Ocho ensayos sobre William Blake, Atalanta, Vilaür 2013; p. 117.
.