![]() « Le savant n’étudie pas la nature parce que cela est utile ; il l’étudie parce qu’il y prend plaisir et il y prend plaisir parce qu’elle est belle. Si la nature n’était pas belle, elle ne vaudrait pas la peine d’être connue, la vie ne vaudrait pas la peine d’être vécue ».
« Le savant n’étudie pas la nature parce que cela est utile ; il l’étudie parce qu’il y prend plaisir et il y prend plaisir parce qu’elle est belle. Si la nature n’était pas belle, elle ne vaudrait pas la peine d’être connue, la vie ne vaudrait pas la peine d’être vécue ».
Jules Henri Poincaré (matemático francés del siglo XIX).
1. Presentación
Desde tiempos inmemoriales el hombre quiere encontrar una explicación al comportamiento y a la estructura del cosmos. Se ha intentado dar una visión más o menos sistemática al medio que nos envuelve y el espacio mítico es una respuesta sentimental e imaginativa a estas necesidades humanas fundamentales.
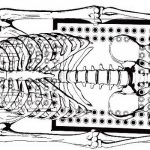
A la pregunta de cómo está relacionado el ser humano con la tierra y el cosmos se le pueden dar dos clases de respuestas, dos esquemas extensamente conocidos en diversas partes del mundo. En un esquema, el cuerpo humano se percibe como una imagen del cosmos, es decir, existe una analogía entre la anatomía humana y la fisonomía de la tierra. En el otro, el hombre es el centro de un marco cósmico orientado hacia los puntos cardinales y con un eje vertical.
El cuerpo humano se percibe como una imagen del cosmos, es decir, existe una analogía entre la anatomía humana y la fisonomía de la tierra.
Respecto al primer esquema, que es el que aquí nos interesa, podemos dar dos ejemplos poco usuales. Los dogón de África ven las rocas como el hueso, la tierra como las partes interiores del estómago y la arcilla roja como la sangre. Tradiciones populares de la China consideran a la tierra como un ser cósmico: las montañas son su cuerpo, las rocas sus huesos, el agua la sangre que corre por las venas, los árboles y la hierba sus cabellos, las nubes y la niebla los vapores de su respiración.

Imágenes aéreas tomadas sobre las zonas del Nilo, el Amazonas y los grandes Lagos. Son superficies de estructura muy irregular que se aproximan a modelos de geometría fractal.
Y pensando más ampliamente, en la Grecia antigua ya existía la creencia de que los dos términos de la pareja macrocosmos (lo que supera la escala humana terrestre) y microcosmos (lo que es igual o inferior a nuestra escala), están relacionados. Esta relación se entendía como una identidad en la que estructuras de uno y otro reproducían las mismas pautas y patrones a todos los niveles, empezando por el macrocosmos o universo y descendiendo hasta el microcosmos. En textos árabes del 650 d. C. se han encontrado transcripciones del segundo precepto de la Tabla de Esmeralda que dice: Lo que está abajo es como lo que está arriba, y lo que está arriba es como lo que está abajo. Con los descubrimientos de los últimos años podemos decir que el paso de lo mítico a lo científico es una frontera más bien borrosa y que este precepto ha sido una visión premonitoria de lo que se ha llamado científicamente Teoría de los Sistemas Complejos y Geometría Fractal.
La Tabla de Esmeralda dice: Lo que está abajo es como lo que está arriba, y lo que está arriba es como lo que está abajo
Thomas Kuhn -físico, historiador y filósofo de la ciencia- propone, en su extraordinaria obra The Structure of Scientific Revolutions, que la ciencia no evoluciona en una progresión gradual hacia el conocimiento. En contra de la visión más generalizada de la época, dice que el conocimiento de la verdad se desarrolla en largos periodos de progreso relativamente tranquilos seguidos de cortos episodios de revolución paradigmática, durante los cuales las teorías se adaptan mejor a la realidad y se generalizan. Según su propia definición, paradigma no es sólo el ejemplo y el modelo sino aquello que se debe observar y el tipo de interrogantes que se supone que se han de formular para llegar al conocimiento. Por ejemplo, tenemos el caso de la mecánica cuántica que durante el primer cuarto del siglo XX substituye a la clásica porque la generaliza y explica fenómenos que ésta era incapaz de explicar. Sucede lo mismo con la teoría de la relatividad einsteiniana respecto a la teoría newtoniana. Cada uno de estos cambios ha supuesto un desplazamiento rápido y revolucionario del pensamiento dentro de su disciplina específica, la física.
2. Los Sistemas complejos y la Geometría fractal
Durante las últimas tres décadas está sucediendo un cambio paradigmático que afecta a todas y a cada una de las disciplinas científicas simultáneamente. Este nuevo paradigma es la Teoría de los Sistemas Complejos y la Geometría Fractal que antes hemos mencionado. Están tan estrechamente relacionadas que se ha llegado a decir de la segunda respecto a la primera que es la mano que mece la cuna. Así, también se ha afirmado que el descubrimiento de la ubicuidad del caos es la tercera revolución de los tiempos actuales, junto con la relatividad y la mecánica cuántica.
Durante las últimas tres décadas está sucediendo un cambio paradigmático que afecta a todas y a cada una de las disciplinas científicas simultáneamente. Este nuevo paradigma es la Teoría de los Sistemas Complejos y la Geometría Fractal
La Geometría (etimológicamente: medida de la tierra) es la disciplina de las matemáticas que estudia la forma de las cosas. ¿Qué es lo que da forma a las cosas? ¿Cómo es posible que se den formas regulares o periódicas, sin la intervención de un diseño impuesto desde fuera; sin un ingeniero que cuide de todos y cada uno de los detalles del diseño? Durante siglos se han buscado leyes que definan el movimiento de los planetas o la forma de los caracoles; se han buscado fórmulas para predecir la caída de un objeto o para estudiar el vuelo de las aves; igualmente se ha estudiado la anatomía de los seres vivos y la estructura de la mente humana. Pero también queremos entender la forma de las galaxias, de las nubes y de las costas, la estructura de las relaciones humanas y del surgimiento y la caída de las civilizaciones, el origen de las guerras y el origen de la vida. Hasta la invención de los sistemas complejos no se había podido dar respuestas satisfactorias a estos últimos interrogantes.
Parece absurdo decir que un objeto es amorfo ya que todo objeto tiene una forma. Una explicación a este aparente contrasentido podría consistir en decir que un objeto es amorfo cuando su apariencia es compleja, irregular y no existe ninguna estructura subyacente. Así los objetos euclidianos como el círculo, el cuadrado, la esfera o el tetraedro tienen una forma bien definida. También los cristales tienen una estructura subyacente bien determinada y conocida que los clasifica matemáticamente. No es propósito de este artículo definir matemáticamente una fractal, pero diremos que es fácilmente reconocible por ser un objeto con una apariencia muy compleja e irregular, en realidad, etimológicamente, fractal viene de fracturado i/o irregular. Un árbol es un ejemplo muy aproximado de lo que es una fractal. El rasgo más importante es la autosimilitud, es decir, una rama por si sola podría ser considerada un árbol en pequeño. En una fractal auténtica (matemáticamente bien definida) la autosimilitud se manifiesta a cualquier escala de observación, hasta lo infinitamente pequeño. Recordemos ahora el precepto que afirmaba que lo que está arriba es como lo que está abajo. Lo de arriba y lo de abajo serían aquí considerados como a gran escala y a pequeña escala.
En una fractal auténtica (matemáticamente bien definida) la autosimilitud se manifiesta a cualquier escala de observación, hasta lo infinitamente pequeño.
Nuestro cuerpo tiene estructuras que pueden ser aproximadas por fractales: el árbol bronquial, las rugosidades interiores del intestino, el sistema circulatorio, la porosidad de los pulmones… La tierra también posee este tipo de estructuras: los ríos con sus afluentes, las rocas porosas de los acantilados, los perfiles irregulares de las montañas y de los continentes… Y también el universo participa de esta fractalidad: sistemas planetarios dentro de sistemas solares, galaxias dentro de cúmulos de galaxias y éstos dentro de supercúmulos.
Es un hecho muy curioso que estudios relacionados con distintos aspectos de islas y continentes han ido muy ligados al avance de la Teoría Fractal. Ya en 1938, Jaromir Korcak hizo unas estadísticas de la distribución de las islas en diferentes regiones de la tierra deduciendo una ley muy interesante. En esta ley interviene un concepto matemático que más tarde se denominará dimensión de Hausdorff, que generaliza la dimensión euclidiana que todos conocemos y que ha resultado ser esencial en la caracterización de las fractales. Así, la dimensión de Hausdorff de una línea es 1, la de una superficie es 2 y la de un volumen es 3, pero se da el caso que la dimensión de Hausdorff de una costa es un número decimal que se encuentra entre 1 y 2 (dependiendo de su irregularidad), y la de una esponja, entre 2 y 3 (dependiendo de la cantidad de agujeros). Cada fractal tiene asociada una dimensión decimal que depende de su irregularidad y grado de fractura. Fijémonos en que fractal y fractura tienen ambas la misma raíz etimológica.
Cada fractal tiene asociada una dimensión decimal que depende de su irregularidad y grado de fractura
Continuando en esta línea, Lewis Fry Richardson, científico y pacifista inglés, al estudiar en 1949 la relación entre la probabilidad de que dos países se declare la guerra y la longitud de la frontera común, descubrió esencialmente la misma ley y el mismo concepto. Observó que países con fronteras comunes, asignan distintas longitudes a las propias fronteras. Por ejemplo, España dice que su frontera con Portugal mide 987 Km, mientras que Portugal dice que esta misma frontera es de 1214 Km. Fry Richardson intenta explicar esas diferencias tan grandes, a veces de más del 20 por ciento, y llega a la conclusión de que no existe una longitud que pueda denominarse auténtica, ya que de hecho, ésta crece hacia el infinito a medida que aumentamos la precisión de la medida. Así la longitud no es una magnitud adecuada para medir objetos muy irregulares, pero sí lo es la dimensión de Hausdorff. En su día, estos descubrimientos fueron ignorados por la comunidad científica, pero actualmente se consideran de vital importancia, ya que impulsaron el estudio moderno de las fractales. Esta investigación fue citada por Mandelbrot en un famoso artículo de 1967 titulado How Long Is the Coast of Britain?
Además de por la dimensión de Haudorff, las fractales se caracterizan por otra propiedad esencial: su recursividad.
Un objeto es recursivo cuando su algoritmo de formación lo es. Aproximadamente podemos decir que un árbol es recursivo puesto que una rama primaria es como la totalidad del árbol, que una rama secundaria es como la primaria y así sucesivamente. Es decir, que una estructura compleja como un árbol no implica necesariamente un mecanismo de formación complicado. De hecho, uno de los objetos más complejos que ha dado la investigación matemática es el conjunto de Mandelbrot. Este conjunto, compuesto por multitud de diversas y bellas formas que parecen aleatorias, está generado por la sencilla operación de elevar al cuadrado los puntos de un plano. Sin duda, este descubrimiento sorprendente de que algunos sistemas deterministas pueden generar aleatoriedad abre el camino a una nueva y aparente paradoja: el caos puede ser determinista, generado por reglas fijas que no incluyen en sí mismas ningún elemento azaroso, y no obstante el azar se produce. Este objeto y en general los relacionados con el caos y las fractales no hubieran podido ser explorados sin los ordenadores, ya que si bien la operación es muy sencilla, debe efectuarse miles de millones de veces.
El caos puede ser determinista, generado por reglas fijas que no incluyen en sí mismas ningún elemento azaroso, y no obstante el azar se produce.
Todo eso nos lleva a pensar que la naturaleza se comporta de forma recursiva en cuanto que la lectura de un código genético genera millones de individuos de aspectos tan diversos. Pero, ¿cuál es la sencilla ley que confluye en esta recursividad? En descubrir esta ley está el reto de la mente humana, y es posible que gracias a estas analogías podamos descubrir la ley universal que genera el cosmos con toda su diversidad y magnificencia.
3. Información del libro
Una nueva manera de ver el mundo Maria Isabel Binimelis Bassa